
When doing math I think about everything as a series of pictures. When writing math I try, and often enjoy, bringing these pictures to life (or at least onto the page).
This is a gallery of some of my favourite figures/math pictures that appear in my papers.
-
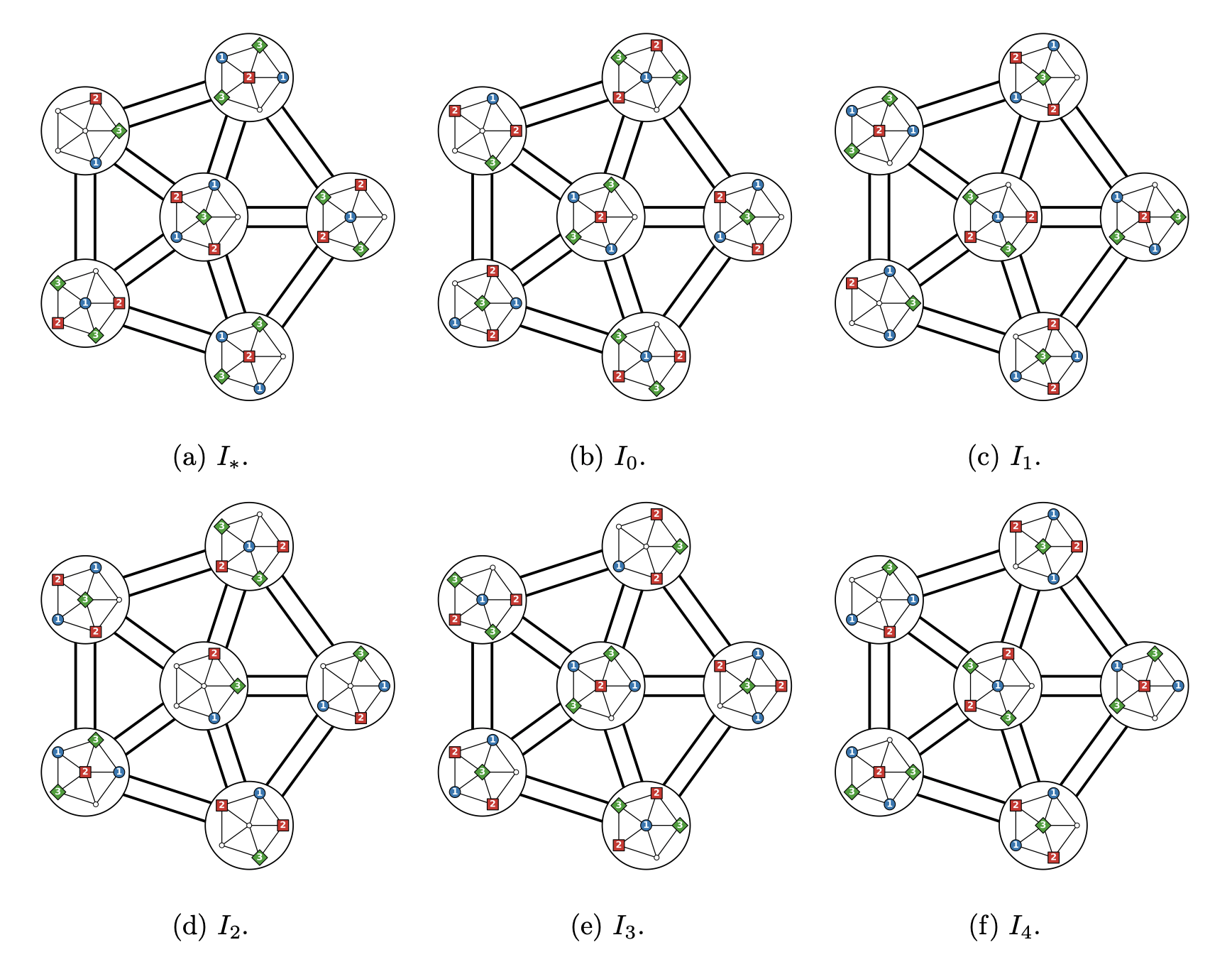
170
A maximum independent set (of size 170) in the third Cartesian power of W_5 Cartesian product with K_3. The independent set is displayed as a maximum 3-colouring of the third Cartesian power of W_5, and the the third Cartesian power of W_5 is displayed as 6 stylised copies of he second Cartesian power of W_5 using the obvious partition.
-
Globally hard to colour, but my paths are easy
A drawing that illustrates howto construct a graph G_{k+1}^r from a graph G_k^r (here r=6 and k=0). When k is small relative to r , the graph G_k^r has chromatic number k+r, while all traceable subgraphs of G_k^r are r-colourable.
-
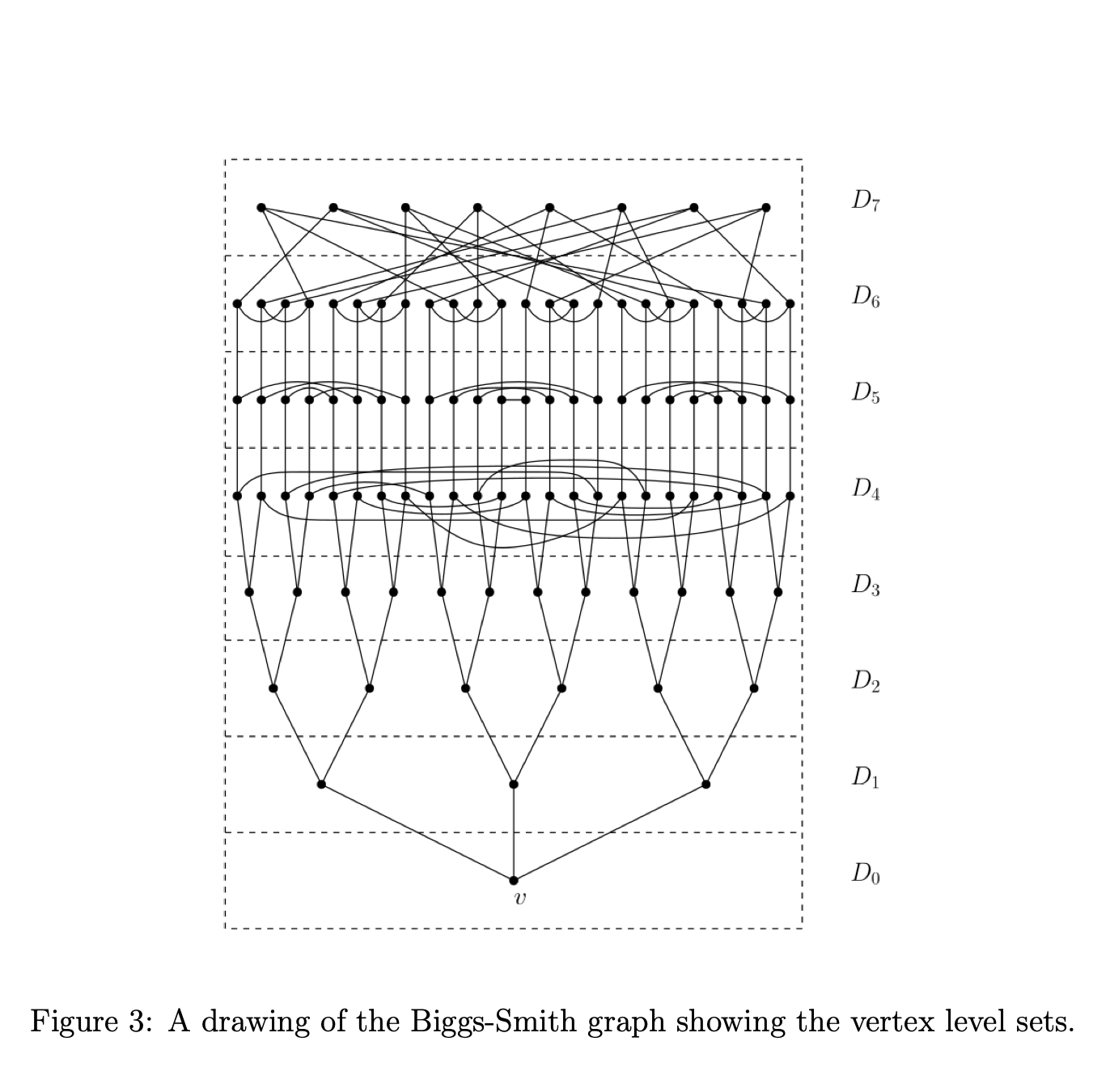
Biggs-Smith level sets
A drawing of the Biggs-Smith graph which partitions its vertices based on their distance to a fixed vertex. Given the graph is vertex transitive, the choice of fixed point is not important.
-
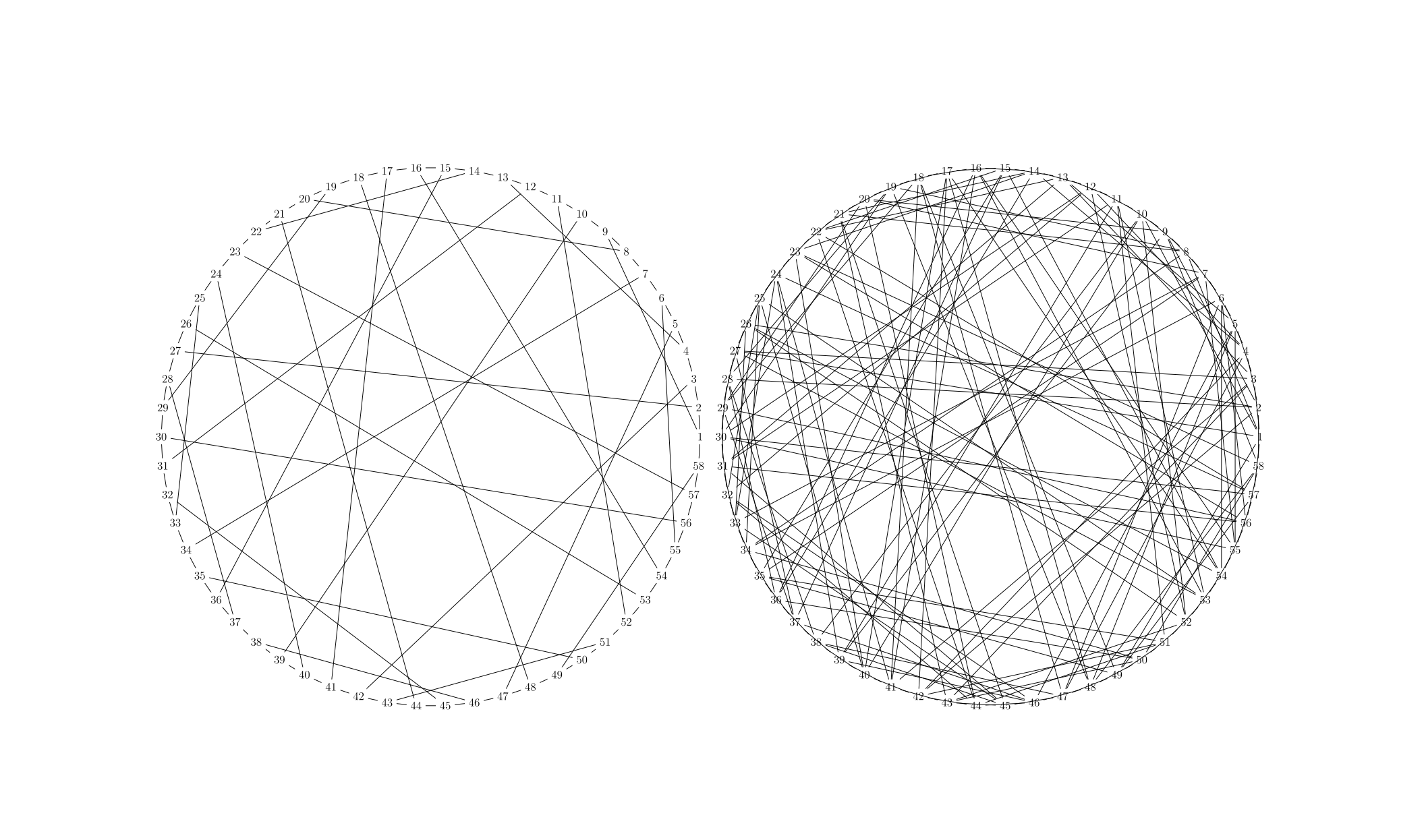
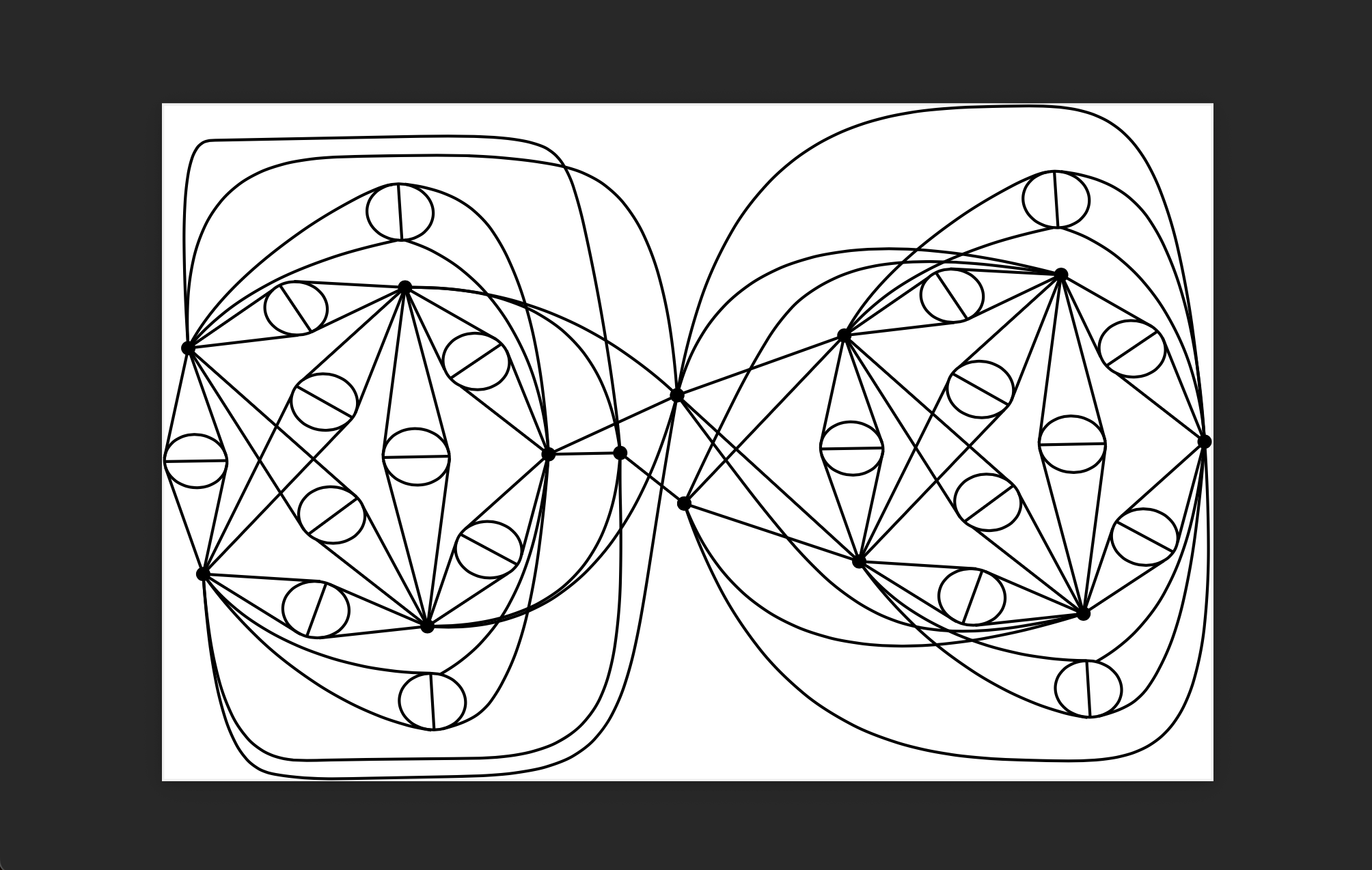
Square me then subtract my edges
The graph on the left is a (3,9)-cage, that is, a smallest (58 vertices) cubic graph with girth 9. The graph on the right is obtained by adding an edge between all vertices of distance exactly 2 on the left.
-
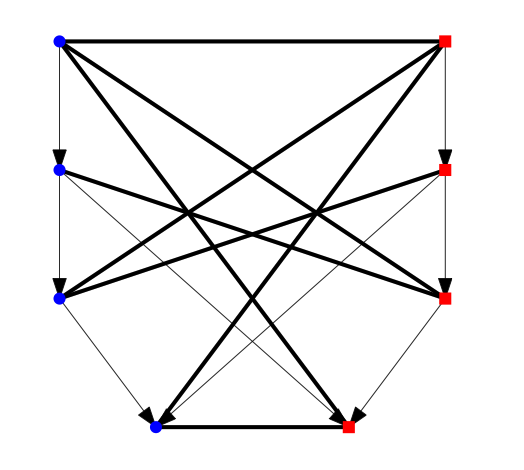
A hard to build game
The digraph shown is a smallest (8 vertex) Digraph Placement game with a particularly hard to construct value. The value is highly symmetric, and this digraph was found by exploiting that symmetry.
-
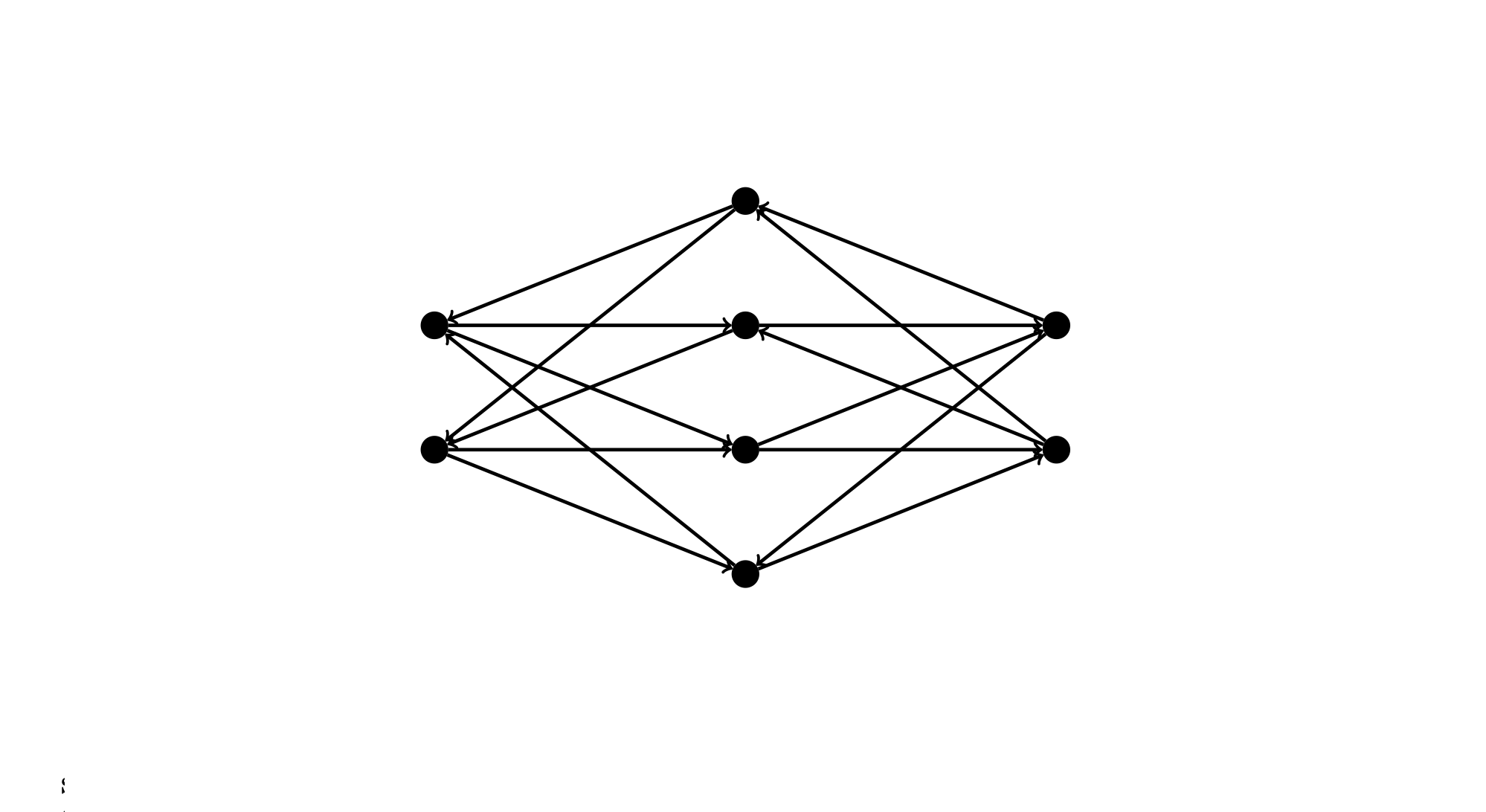
A (2,2,4)-full graph
An orientation of K_{4,4} such that for all pairs of vertices in either bipartition, and all possible orientations to a third vertex, such an orientation exists.
-
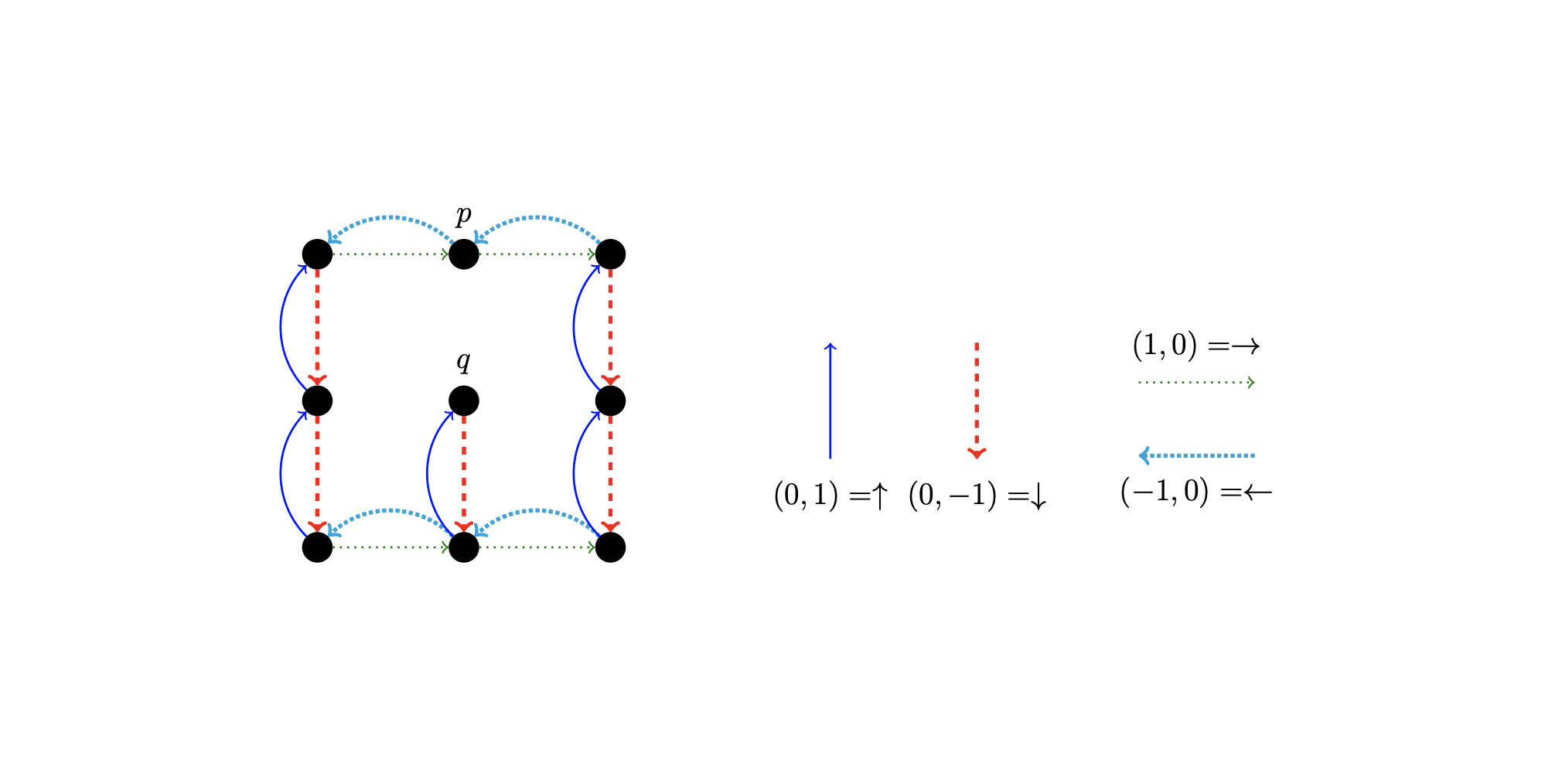
A cute little automata
This deterministic finite automata demonstrates that ‘movement automata’ in 2-dimensions can be periodic . The word (left,down,right,down,right,up,up,left) swaps states p and q.
-
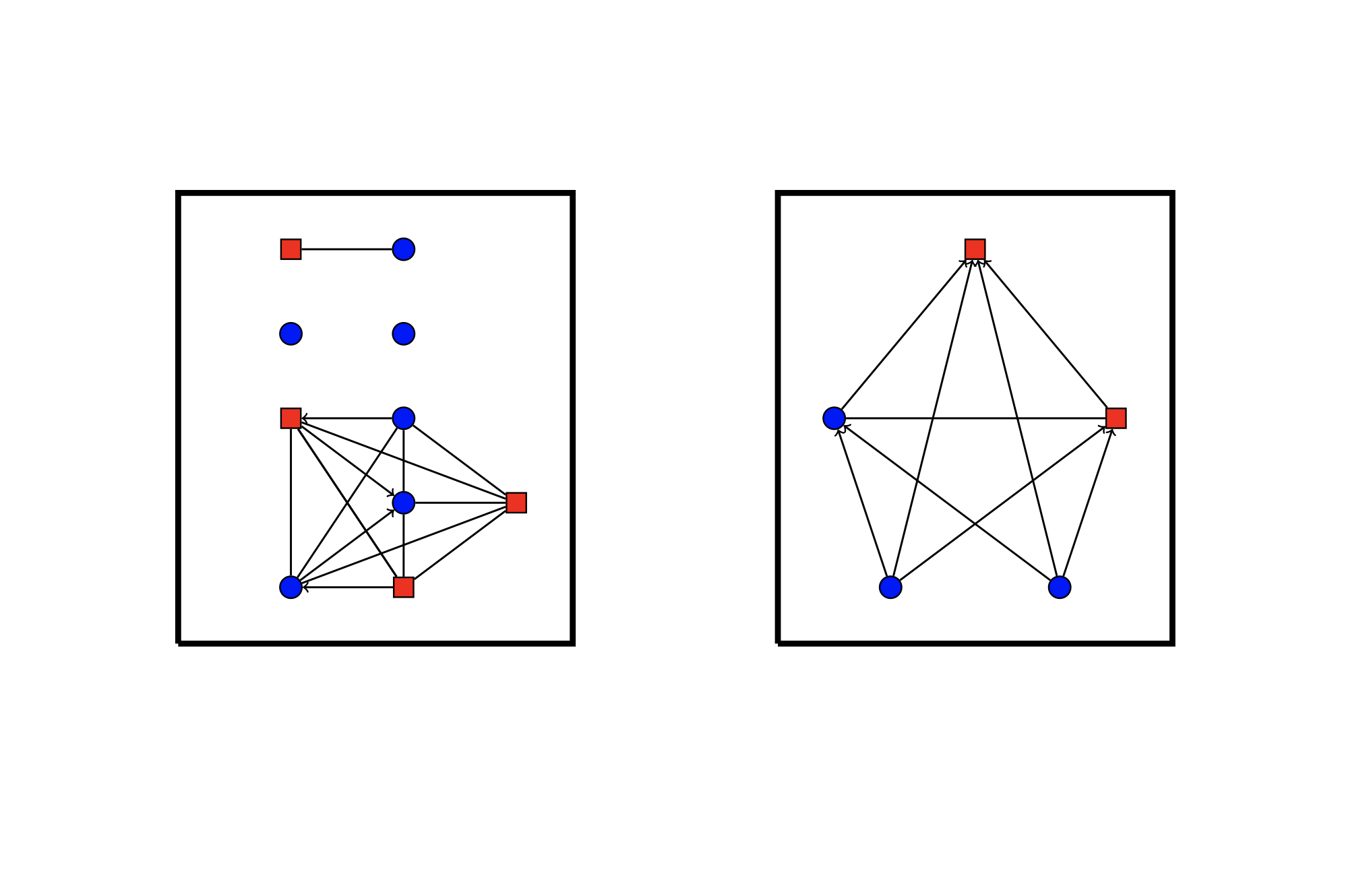
Equality doesn’t mean similarity
Two Digraph placement games that have the same value, but whose underlying digraphs are not very similar.
-
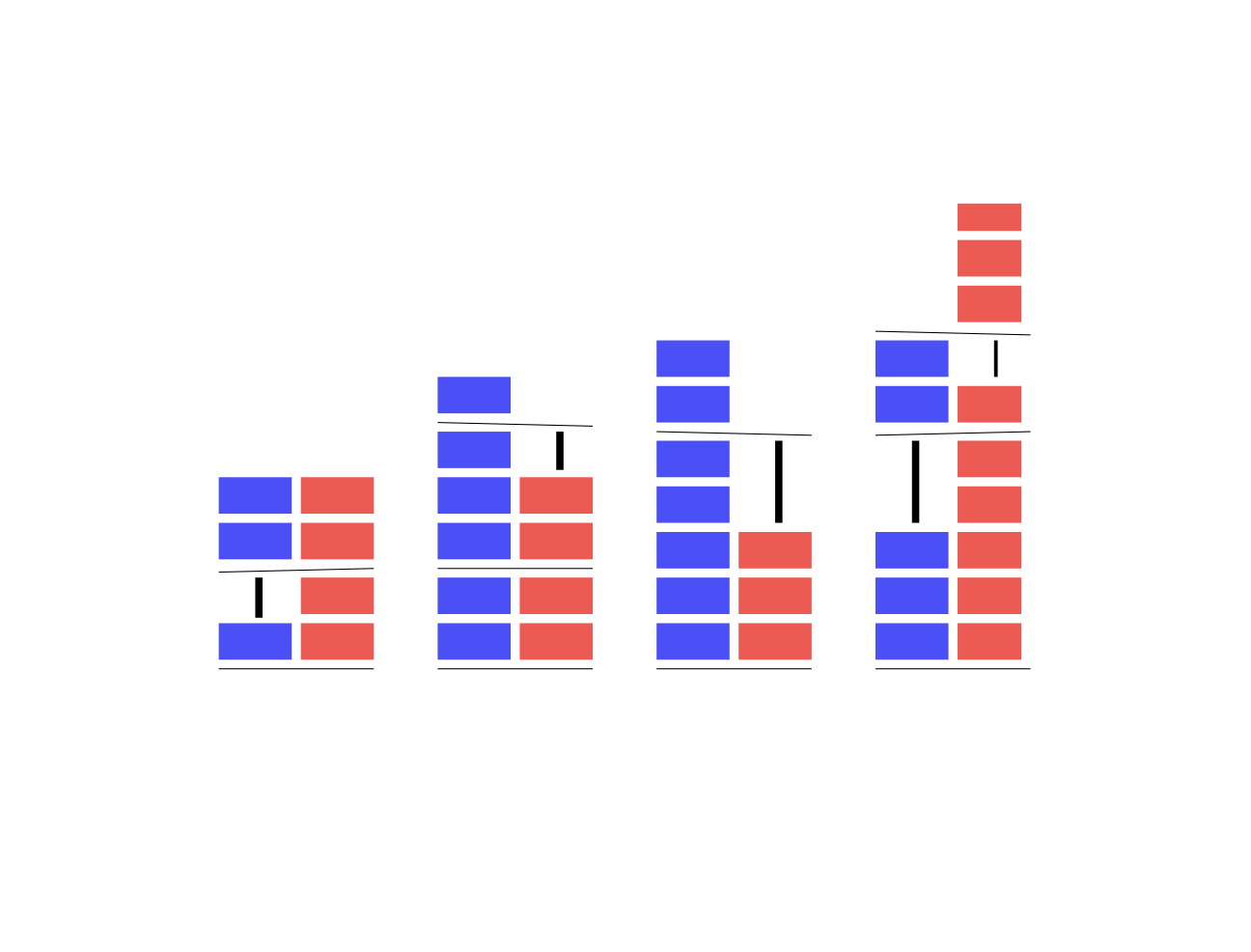
Teetering Towers
A position in the game teetering towers. This position exists to demonstrate why the form of games, not just their values, matter in a disjunctive sum of ordinal sums.

